NCERT Class 8 Maths Chapter 7 Cubes and Cube Roots Solutions
NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Exercise 7.1
Ex 7.1 Class 8 Maths Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) Prime factorisation of 216 is:
216 = 2 × 2 × 2 × 3 × 3 × 3
In the above factorisation, 2 and 3 have formed a group of three.
Thus, 216 is a perfect cube.
(ii) Prime factorisation of 128 is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, 2 is left without making a group of three.
Thus 128 is not a perfect cube.
(iii) Prime factorisation of 1000, is:
1000 = 2 × 2 × 2 × 5 × 5 × 5
Here, no number is left for making a group of three.
Thus, 1000 is a perfect cube.
(iv) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here 2 and 5 have not formed a group of three.
Thus, 100 is not a perfect cube.
(v) Prime factorisation of 46656 is:
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Here 2 and 3 have formed the groups of three.
Thus, 46656 is a perfect cube.
Ex 7.1 Class 8 Maths Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
(i) Prime factorisation of 243, is:
243 = 3 × 3 × 3 × 3 × 3 = 33 × 3 × 3
Here, number 3 is required to make 3 × 3 a group of three, i.e., 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.
(ii) Prime factorisation of 256, is:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2 × 2
Here, a number 2 is needed to make 2 × 2 a group of three, i.e., 2 × 2 × 2
Thus, the required smallest number to be multiplied is 2.
(iii) Prime factorisation of 72, is:
72 = 2 × 2 × 2 × 3 × 3 = 23 × 3 × 3
Here, a number 3 is required to make 3 × 3 a group of three, i.e. 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.
(iv) Prime factorisation of 675, is:
675 = 3 × 3 × 3 × 5 × 5 = 33 × 5 × 5
Here, a number 5 is required to make 5 × 5 a group of three to make it a perfect cube, i.e. 5 × 5 × 5
Thus, the required smallest number is 5.
(v) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here, number 2 and 5 are needed to multiplied 2 × 2 × 5 × 5 to make it a perfect cube, i.e., 2 × 2 × 2 × 5 × 5 × 5
Thus, the required smallest number to be multiplied is 2 × 5 = 10.
Ex 7.1 Class 8 Maths Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 92
(v) 704
Solution:
(i) Prime factorisation of 81, is:
81 = 3 × 3 × 3 × 3 = 33 × 3
Here, a number 3 is the number by which 81 is divided to make it a perfect cube,
i.e., 81 ÷ 3 = 27 which is a perfect cube.
Thus, the required smallest number to be divided is 3.
(ii) Prime factorisation of 128, is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2
Here, a number 2 is the smallest number by which 128 is divided to make it a perfect cube,
i.e., 128 ÷ 2 = 64 which is a perfect cube.
Thus, 2 is the required smallest number.
(iii) Prime factorisation of 135 is:
135 = 3 × 3 × 3 × 5 = 33 × 5
Here, 5 is the smallest number by which 135 is divided to make a perfect cube,
i.e., 135 ÷ 5 = 27 which is a perfect cube.
Thus, 5 is the required smallest number.
(iv) Prime factorisation of 192 is:
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 23 × 23 × 3
Here, 3 is the smallest number by which 192 is divided to make it a perfect cube,
i.e., 192 ÷ 3 = 64 which is a perfect cube.
Thus, 3 is the required smallest number.
(v) Prime factorisation of 704 is:
704 = 2 × 2 × 2 × 2 × 2 × 2 × 11 = 23 × 23 × 11
Here, 11 is the smallest number by which 704 is divided to make it a perfect cube,
i.e., 704 ÷ 11 = 64 which is a perfect cube.
Thus, 11 is the required smallest number.
Ex 7.1 Class 8 Maths Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will be needed to form a cube?
Solution:
The sides of the cuboid are given as 5 cm, 2 cm and 5 cm.
Volume of the cuboid = 5 cm × 2 cm × 5 cm = 50 cm3
For the prime factorisation of 50, we have
50 = 2 × 5 × 5
To make it a perfect cube, we must have
2 × 2 × 2 × 5 × 5 × 5
= 20 × (2 × 5 × 5)
= 20 × volume of the given cuboid
Thus, the required number of cuboids = 20.




Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2
NCERT Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2 Solutions
NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Exercise 7.2
Ex 7.2 Class 8 Maths Question 1.
Find the cube root of each of the following numbers by prime factorisation method.
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution:






Ex 7.2 Class 8 Maths Question 2.
State True or False.
(i) Cube of an odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If the square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution:
(i) False – Cube of any odd number is always odd, e.g., (7)3 = 343
(ii) True – A perfect cube does not end with two zeros.
(iii) True – If a square of a number ends with 5, then its cube ends with 25, e.g., (5)2 = 25 and (5)3 = 625
(iv) False – (12)3 = 1728 (ends with 8)
(v) False – (10)3 = 1000 (4-digit number)
(vi) False – (99)3 = 970299 (6-digit number)
(vii) True – (2)3 = 8 (1-digit number)
Ex 7.2 Class 8 Maths Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution:
The given perfect cube = 1331
Forming groups of three from the rightmost digits of 1331
IInd group = 1
1st group = 331
One’s digit in first group = 1
One’s digit in the required cube root may be 1.
The second group has only 1.
Estimated cube root of 1331 = 11
Thus = 11
(i) Given perfect cube = 4913
Forming groups of three from the right most digit of 4913
IInd group = 4
1st group = 913
One’s place digit in 913 is 3.
One’s place digit in the cube root of the given number may be 7.
Now in IInd group digit is 4
13 < 4 < 23
Ten’s place must be the smallest number 1.
Thus, the estimated cube root of 4913 = 17.
(ii) Given perfect cube = 12167
Forming group of three from the rightmost digits of 12167
We have IInd group = 12
1st group = 167
The ones place digit in 167 is 7.
One’s place digit in the cube root of the given number may be 3.
Now in Ilnd group, we have 12
23 < 12 < 33
Ten’s place of the required cube root of the given number = 2.
Thus, the estimated cube root of 12167 = 23.
(iii) Given perfect cube = 32768
Forming groups of three from the rightmost digits of 32768, we have
IInd group = 32
1st group = 768
One’s place digit in 768 is 8.
One’s place digit in the cube root of the given number may be 2.
Now in IInd group, we have 32
33 < 32 < 43
Ten’s place of the cube root of the given number = 3.
Thus, the estimated cube root of 32768 = 32.







Extra Questions
Cubes and Cube Roots Class 8 Extra Questions Maths Chapter 7
Extra Questions for Class 8 Maths Chapter 7 Cubes and Cube Roots
Cubes and Cube Roots Class 8 Extra Questions Very Short Answer Type
Question 1.
Find the cubes of the following:
(a) 12
(b) -6
(c)
(d)
Solution:
Question 2.
Find the cubes of the following:
(a) 0.3
(b) 0.8
(c) .001
(d) 2 – 0.3
Sol.
(a) (0.3)3 = 0.3 × 0.3 × 0.3 = 0.027
(b) (0.8)3 = 0.8 × 0.8 × 0.8 = 0.512
(c) (0.001)3 = (0.001) × (0.001) × (0.001) = 0.000000001
(d) (2 – 0.3)3 = (1.7)3 = 1.7 × 1.7 × 1.7 = 4.913
Question 3.
Is 135 a perfect cube?
Solution:
Prime factorisation of 135, is:
135 = 3 × 3 × 3 × 5
We find that on making triplet, the number 5 does not make a group of the triplet.
Hence, 135 is not a perfect cube.
Question 4.
Find the cube roots of the following:
(a) 1728
(b) 3375
Solution:

Question 5.
Examine if (i) 200 (ii) 864 are perfect cubes.
Solution:
(i) 200 = 2 × 2 × 2 × 5 × 5
If we form triplet of equal factors, the number 2 forms a group of three whereas 5 does not do it.
Therefore, 200 is not a perfect cube.
(ii) We have 864 = 2 × 2 × 2 × 2 × 2
If we form triplet of equal factors, the number 2 and 3 form a group of three whereas another group of 2’s does not do so.
Therefore, 864 is not a perfect cube.
Question 6.
Find the smallest number by which 1323 may be multiplied so that the product is a perfect cube.
Solution:
1323 = 3 × 3 × 3 × 7 × 7
Since we required one more 7 to make a triplet of 7.
Therefore 7 is the smallest number by which 1323 may be multiplied to make it a perfect cube.
Question 7.
What is the smallest number by which 2916 should be divided so that the quotient is a perfect cube?
Solution:
Prime factorisation of
2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Since we required one more 2 to make a triplet
Therefore, the required smallest number by which 2916 should be divided to make it a perfect cube is 2 × 2 = 4, i.e., 2916 ÷ 4 = 729 which is a perfect cube.
Question 8.
Check whether 1728 is a perfect cube by using prime factorisation. (NCERT Exemplar)
Solution:
Prime factorisation of 1728 is
1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
Since all prime factors can be grouped in triplets.
Therefore, 1728 is a perfect cube.
Question 9.
Using prime factorisation, find the cube root of 5832. (NCERT Exemplar)
Solution:
Question 10.![]()
Solution:
Cubes and Cube Roots Class 8 Extra Questions Short Answers Type
Question 11.
Solution:

Question 12.
Find the cube roots of
(i) 4
(ii) -0.729
Solution:
Question 13.
Express the following numbers as the sum of odd numbers using the given pattern
Solution:
Question 14.
Observe the following pattern and complete the blank spaces.
13 = 1
Solution:
















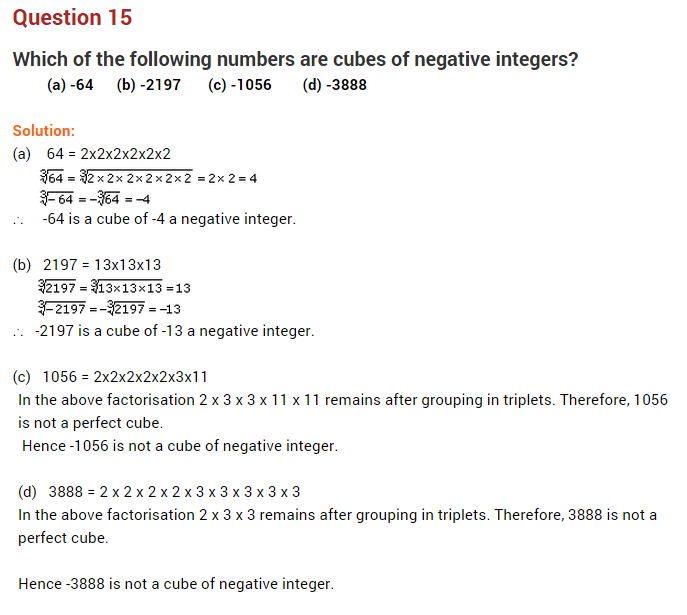





NCERT Solutions for Class 8 Maths
- Chapter 1: Rational Numbers
- Chapter 2: Linear Equations in One Variable
- Chapter 3: Understanding Quadrilaterals
- Chapter 4: Practical Geometry
- Chapter 5: Data Handling
- Chapter 6: Squares and Square Roots
- Chapter 7: Cubes and Cube Roots
- Chapter 8: Comparing Quantities
- Chapter 9: Algebraic Expressions and Identities
- Chapter 10: Visualising Solid Shapes
- Chapter 11: Mensuration
- Chapter 12: Exponents and Powers
- Chapter 13: Direct and Indirect proportions
- Chapter 14: Factorisation
- Chapter 15: Introduction to Graphs
- Chapter 16: Playing with Numbers


