NCERT Class 8 Maths Chapter 6 Squares and Square Roots Solutions

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.1

Ex 6.1 Class 8 Maths Question 1.
What will be the unit digit of the squares of the following numbers?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 20387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Solution:
(i) Unit digit of 81² = 1
(ii) Unit digit of 272² = 4
(iii) Unit digit of 799² = 1
(iv) Unit digit of 3853² = 9
(v) Unit digit of 1234² = 6
(vi) Unit digit of 26387² = 9
(vii) Unit digit of 52698² = 4
(viii) Unit digit of 99880² = 0
(ix) Unit digit of 12796² = 6
(x) Unit digit of 55555² = 5

Ex 6.1 Class 8 Maths Question 2.
The following numbers are not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
Solution:
(i) 1057 ends with 7 at unit place. So it is not a perfect square number.
(ii) 23453 ends with 3 at unit place. So it is not a perfect square number.
(iii) 7928 ends with 8 at unit place. So it is not a perfect square number.
(iv) 222222 ends with 2 at unit place. So it is not a perfect square number.
(v) 64000 ends with 3 zeros. So it cannot a perfect square number.
(vi) 89722 ends with 2 at unit place. So it is not a perfect square number.
(vii) 22000 ends with 3 zeros. So it can not be a perfect square number.
(viii) 505050 ends with 1 zero. So it is not a perfect square number.

Ex 6.1 Class 8 Maths Question 3.
The squares of which of the following would be odd numbers?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Solution:
(i) 431² is an odd number.
(ii) 2826² is an even number.
(iii) 7779² is an odd number.
(iv) 82004² is an even number.

Ex 6.1 Class 8 Maths Question 4.
Observe the following pattern and find the missing digits.
11² = 121
101² = 10201
1001² = 1002001
100001² = 1…2…1
10000001² = ………
Solution:
According to the above pattern, we have
100001² = 10000200001
10000001² = 100000020000001

Ex 6.1 Class 8 Maths Question 5.
Observe the following pattern and supply the missing numbers.
11² = 121
101² = 10201
10101² = 102030201
1010101² = ……….
……….² = 10203040504030201
Solution:
According to the above pattern, we have
1010101² = 1020304030201
101010101² = 10203040504030201

Ex 6.1 Class 8 Maths Question 6.
Using the given pattern, find the missing numbers.
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + ….² = 21²
5² + ….² + 30² = 31²
6² + 7² + …..² = ……²
Solution:
According to the given pattern, we have
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
6² + 7² + 42² = 43²

Ex 6.1 Class 8 Maths Question 7.
Without adding, find the sum.
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Solution:
We know that the sum of n odd numbers = n²
(i) 1 + 3 + 5 + 7 + 9 = (5)² = 25 [∵ n = 5]
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = (10)² = 100 [∵ n = 10]
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = (12)² = 144 [∵ n = 12]

Ex 6.1 Class 8 Maths Question 8.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Solution:
(i) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 (n = 7)
(ii) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 (n = 11)

Ex 6.1 Class 8 Maths Question 9.
How many numbers lie between squares of the following numbers?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution:
(i) We know that numbers between n² and (n + 1)² = 2n
Numbers between 12² and 13² = (2n) = 2 × 12 = 24
(ii) Numbers between 25² and 26² = 2 × 25 = 50 (∵ n = 25)
(iii) Numbers between 99² and 100² = 2 × 99 = 198 (∵ n = 99)

Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2 Solutions

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.2

Ex 6.2 Class 8 Maths Question 1.
Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Solution:
(i) 32 = 30 + 2
(32)² = (30 + 2)²
= 30(30 + 2) + 2(30 + 2)
= 30² + 30 × 2 + 2 × 30 + 2²
= 900 + 60 + 60 + 4
= 1024
Thus (32)² = 1024

(ii) 35 = (30 + 5)
(35)² = (30 + 5)²
= 30(30 + 5) + 5(30 + 5)
= (30)² + 30 × 5 + 5 × 30 + (5)²
= 900 + 150 + 150 + 25
= 1225
Thus (35)² = 1225

(iii) 86 = (80 + 6)
86² = (80 + 6)²
= 80(80 + 6) + 6(80 + 6)
= (80)² + 80 × 6 + 6 × 80 + (6)²
= 6400 + 480 + 480 + 36
= 7396
Thus (86)² = 7396

(iv) 93 = (90+ 3)
93² = (90 + 3)²
= 90 (90 + 3) + 3(90 + 3)
= (90)² + 90 × 3 + 3 × 90 + (3)²
= 8100 + 270 + 270 + 9
= 8649
Thus (93)² = 8649

(v) 71 = (70 + 1)
71² = (70 + 1)²
= 70 (70 + 1) + 1(70 + 1)
= (70)² + 70 × 1 + 1 × 70 + (1)²
= 4900 + 70 + 70 + 1
= 5041
Thus (71)² = 5041

(vi) 46 = (40+ 6)
46² = (40 + 6)²
= 40 (40 + 6) + 6(40 + 6)
= (40)² + 40 × 6 + 6 × 40 + (6)²
= 1600 + 240 + 240 + 36
= 2116
Thus (46)² = 2116

Ex 6.2 Class 8 Maths Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution:
(i) Let m² – 1 = 6
[Triplets are in the form 2m, m² – 1, m² + 1]
m² = 6 + 1 = 7
So, the value of m will not be an integer.
Now, let us try for m² + 1 = 6
⇒ m² = 6 – 1 = 5
Also, the value of m will not be an integer.
Now we let 2m = 6 ⇒ m = 3 which is an integer.
Other members are:
m² – 1 = 3² – 1 = 8 and m² + 1 = 3² + 1 = 10
Hence, the required triplets are 6, 8 and 10

(ii) Let m² – 1 = 14 ⇒ m² = 1 + 14 = 15
The value of m will not be an integer.
Now take 2m = 14 ⇒ m = 7 which is an integer.
The member of triplets are 2m = 2 × 7 = 14
m² – 1 = (7)² – 1 = 49 – 1 = 48
and m² + 1 = (7)² + 1 = 49 + 1 = 50
i.e., (14, 48, 50)

(iii) Let 2m = 16 m = 8
The required triplets are 2m = 2 × 8 = 16
m² – 1 = (8)² – 1 = 64 – 1 = 63
m² + 1 = (8)² + 1 = 64 + 1 = 65
i.e., (16, 63, 65)

(iv) Let 2m = 18 ⇒ m = 9
Required triplets are:
2m = 2 × 9 = 18
m² – 1 = (9)² – 1 = 81 – 1 = 80
and m² + 1 = (9)² + 1 = 81 + 1 = 82
i.e., (18, 80, 82)

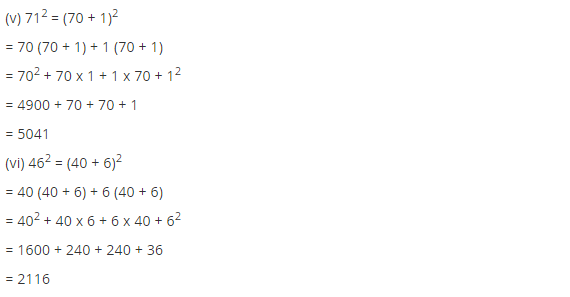
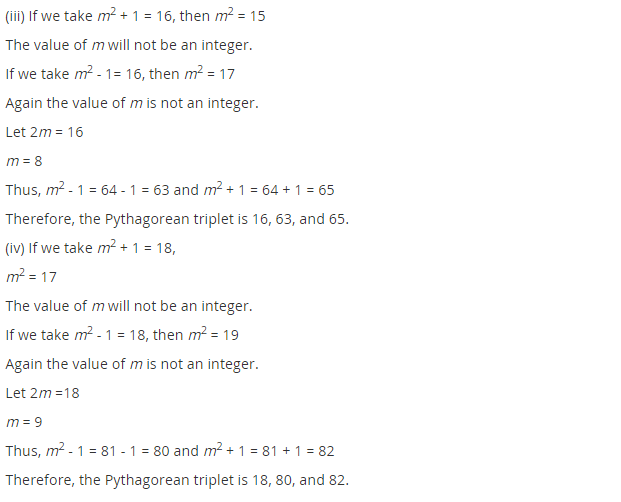
Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.3

Ex 6.3 Class 8 Maths Question 1.
What could be the possible ‘one’s’ digits of the square root of each of the following numbers?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
Solution:
(i) One’s digit in the square root of 9801 maybe 1 or 9.
(ii) One’s digit in the square root of 99856 maybe 4 or 6.
(iii) One’s digit in the square root of 998001 maybe 1 or 9.
(iv) One’s digit in the square root of 657666025 can be 5.

Ex 6.3 Class 8 Maths Question 2.
Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
(iv) 441
Solution:
We know that the numbers ending with 2, 3, 7 or 8 are not perfect squares.
(i) 153 is not a perfect square number. (ending with 3)
(ii) 257 is not a perfect square number. (ending with 7)
(iii) 408 is not a perfect square number. (ending with 8)
(iv) 441 is a perfect square number.

Ex 6.3 Class 8 Maths Question 3.
Find the square roots of 100 and 169 by the method of repeated subtraction.
Solution:
Using the method of repeated subtraction of consecutive odd numbers, we have
(i) 100 – 1 = 99, 99 – 3 = 96, 96 – 5 = 91, 91 – 7 = 84, 84 – 9 = 75, 75 – 11 = 64, 64 – 13 = 51, 51 – 15 = 36, 36 – 17 = 19, 19 – 19 = 0
(Ten times repetition)
Thus √100 = 10

(ii) 169 – 1 = 168, 168 – 3 = 165, 165 – 5 = 160, 160 – 7 = 153, 153 – 9 = 144, 144 – 11 = 133, 133 – 13 = 120, 120 – 15 = 105, 105 – 17 = 88, 88 – 19 = 69, 69 – 21 = 48, 48 – 23 = 25, 25 – 25 = 0
(Thirteen times repetition)
Thus √169 = 13

Ex 6.3 Class 8 Maths Question 4.
Find the square roots of the following numbers by the prime factorisation Method.
(i) 729
(ii) 400
(iii) 1764
(iv) 4096
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Solution:
(i) We have 729
Prime factors of 729
729 = 3 × 3 × 3 × 3 × 3 × 3 = 3² × 3² × 3²
√729 = 3 × 3 × 3 = 27

(ii) We have 400
Prime factors of 400
400 = 2 × 2 × 2 × 2 × 5 × 5 = 2² × 2² × 5²
√400 = 2 × 2 × 5 = 20

(iii) 1764
1764 = 2 × 2 × 3 × 3 × 7 × 7 = 2² × 3² × 7²
√1764 = 2 × 3 × 7 = 42

(iv) 4096
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2² × 2² × 2² × 2² × 2² × 2²
√4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64

(v) Prime factorisation of 7744 is
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
= 2² × 2² × 2² × 11²
√7744 = 2 × 2 × 2 × 11 = 88

(vi) Prime factorisation of 9604 is
9604 = 2 × 2 × 7 × 7 × 7 × 7 = 2² × 7² × 7²
√9604 = 2 × 7 × 7 = 98

(vii) Prime factorisation of 5929 is
5929 = 7 × 7 × 11 × 11 = 7² × 11²
√5929 = 7 × 11 = 77

(viii) Prime factorisation of 9216 is
9216 = 2 × 2 × 2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 3 × 3
= 2² × 2² × 2² × 2² × 2² × 3²
√9216 = 2 × 2 × 2 × 2 × 2 × 3 = 96

(ix) Prime factorisation of 529 is
529 = 23 × 23 = 23²
√529 = 23

(x) Prime factorisation of 8100 is
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 = 2² × 3² × 3² × 5²
√8100 = 2 × 3 × 3 × 5 = 90

Ex 6.3 Class 8 Maths Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also, find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution:
(i) Prime factorisation of 252 is
252 = 2 × 2 × 3 × 3 × 7
Here, the prime factorisation is not in pair. 7 has no pair.
Thus, 7 is the smallest whole number by which the given number is multiplied to get a perfect square number.
The new square number is 252 × 7 = 1764
Square root of 1764 is
√1764 = 2 × 3 × 7 = 42

(ii) Primp factorisation of 180 is
180 = 2 × 2 × 3 × 3 × 5
Here, 5 has no pair.
New square number = 180 × 5 = 900
The square root of 900 is
√900 = 2 × 3 × 5 = 30
Thus, 5 is the smallest whole number by which the given number is multiplied to get a square number.

(iii) Prime factorisation of 1008 is
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
Here, 7 has no pair.
New square number = 1008 × 7 = 7056
Thus, 7 is the required number.
Square root of 7056 is
√7056 = 2 × 2 × 3 × 7 = 84

(iv) Prime factorisation of 2028 is
2028 = 2 × 2 × 3 × 13 × 13
Here, 3 is not in pair.
Thus, 3 is the required smallest whole number.
New square number = 2028 × 3 = 6084
Square root of 6084 is
√6084 = 2 × 13 × 3 = 78

(v) Prime factorisation of 1458 is
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
Here, 2 is not in pair.
Thus, 2 is the required smallest whole number.
New square number = 1458 × 2 = 2916
Square root of 1458 is
√2916 = 3 × 3 × 3 × 2 = 54

(vi) Prime factorisation of 768 is
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, 3 is not in pair.
Thus, 3 is the required whole number.
New square number = 768 × 3 = 2304
Square root of 2304 is
√2304 = 2 × 2 × 2 × 2 × 3 = 48

Ex 6.3 Class 8 Maths Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also, find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution:
(i) Prime factorisation of 252 is
252 = 2 × 2 × 3 × 3 × 7
Here 7 has no pair.
7 is the smallest whole number by which 252 is divided to get a square number.
New square number = 252 ÷ 7 = 36
Thus, √36 = 6

(ii) Prime factorisation of 2925 is
2925 = 3 × 3 × 5 × 5 × 13
Here, 13 has no pair.
13 is the smallest whole number by which 2925 is divided to get a square number.
New square number = 2925 ÷ 13 = 225
Thus √225 = 15

(iii) Prime factorisation of 396 is
396 = 2 × 2 × 3 × 3 × 11
Here 11 is not in pair.
11 is the required smallest whole number by which 396 is divided to get a square number.
New square number = 396 ÷ 11 = 36
Thus √36 = 6

(iv) Prime factorisation of 2645 is
2645 = 5 × 23 × 23
Here, 5 is not in pair.
5 is the required smallest whole number.
By which 2645 is multiplied to get a square number
New square number = 2645 ÷ 5 = 529
Thus, √529 = 23

(v) Prime factorisation of 2800 is
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
Here, 7 is not in pair.
7 is the required smallest number.
By which 2800 is multiplied to get a square number.
New square number = 2800 ÷ 7 = 400
Thus √400 = 20

(vi) Prime factorisation of 1620 is
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5
Here, 5 is not in pair.
5 is the required smallest prime number.
By which 1620 is multiplied to get a square number = 1620 ÷ 5 = 324
Thus √324 = 18

Ex 6.3 Class 8 Maths Question 7.
The students of class VIII of a school donated ₹ 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Total amount of money donated = ₹ 2401
Total number of students in the class = √2401
= 
= 
= 7 × 7
= 49

Ex 6.3 Class 8 Maths Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Total number of rows = Total number of plants in each row = √2025
= 
= 
= 3 × 3 × 5
= 45
Thus the number of rows and plants = 45

Ex 6.3 Class 8 Maths Question 9.
Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Solution:
LCM of 4, 9, 10 = 180
The least number divisible by 4, 9 and 10 = 180
Now prime factorisation of 180 is
180 = 2 × 2 × 3 × 3 × 5
Here, 5 has no pair.
The required smallest square number = 180 × 5 = 900

Ex 6.3 Class 8 Maths Question 10.
Find the smallest number that is divisible by each of the numbers 8, 15 and 20.
Solution:
The smallest number divisible by 8, 15 and 20 is equal to their LCM.
LCM = 2 × 2 × 2 × 3 × 5 = 120
Here, 2, 3 and 5 have no pair.
The required smallest square number = 120 × 2 × 3 × 5 = 120 × 30 = 3600

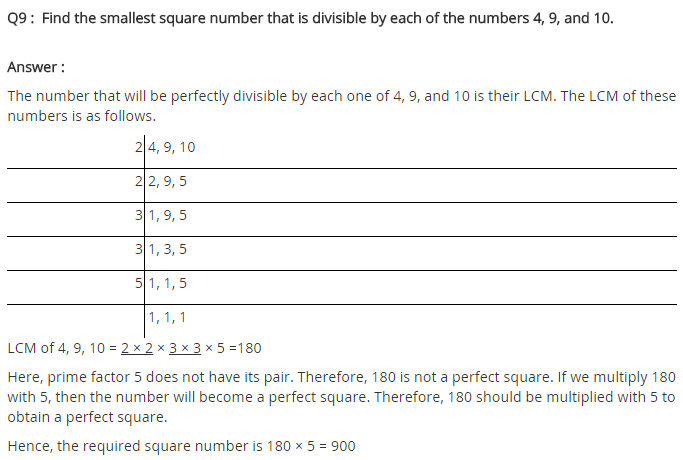
Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4

NCERT Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.4

Ex 6.4 Class 8 Maths Question 1.
Find the square root of each of the following numbers by Long Division method.
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
Solution:

Ex 6.4 Class 8 Maths Question 2.
Find the number of digits in the square root of each of the following numbers (without any calculation)
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625
Solution:
We know that if n is number of digits in a square number then
Number of digits in the square root =  if n is even and  if n is odd.
(i) 64
Here n = 2 (even)
Number of digits in √64 =  = 1
(ii) 144
Here n = 3 (odd)
Number of digits in square root =  = 2
(iii) 4489
Here n = 4 (even)
Number of digits in square root =  = 2
(iv) 27225
Here n = 5 (odd)
Number of digits in square root =  = 3
(iv) 390625
Here n = 6 (even)
Number of digits in square root =  = 3

Ex 6.4 Class 8 Maths Question 3.
Find the square root of the following decimal numbers.
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution:

Ex 6.4 Class 8 Maths Question 4.
Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Solution:
(i)

Here remainder is 2
2 is the least required number to be subtracted from 402 to get a perfect square
New number = 402 – 2 = 400
Thus, √400 = 20

(ii)

Here remainder is 53
53 is the least required number to be subtracted from 1989.
New number = 1989 – 53 = 1936
Thus, √1936 = 44

(iii)

Here remainder is 1
1 is the least required number to be subtracted from 3250 to get a perfect square.
New number = 3250 – 1 = 3249
Thus, √3249 = 57

(iv)

Here, the remainder is 41
41 is the least required number which can be subtracted from 825 to get a perfect square.
New number = 825 – 41 = 784
Thus, √784 = 28

(v)

Here, the remainder is 31
31 is the least required number which should be subtracted from 4000 to get a perfect square.
New number = 4000 – 31 = 3969
Thus, √3969 = 63

Ex 6.4 Class 8 Maths Question 5.
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also, find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Solution:
(i)

Here remainder is 41
It represents that square of 22 is less than 525.
Next number is 23 an 23² = 529
Hence, the number to be added = 529 – 525 = 4
New number = 529
Thus, √529 = 23

(ii)

Here the remainder is 69
It represents that square of 41 is less than in 1750.
The next number is 42 and 42² = 1764
Hence, number to be added to 1750 = 1764 – 1750 = 14
Require perfect square = 1764
√1764 = 42

(iii)

Here the remainder is 27.
It represents that a square of 15 is less than 252.
The next number is 16 and 16² = 256
Hence, number to be added to 252 = 256 – 252 = 4
New number = 252 + 4 = 256
Required perfect square = 256
and √256 = 16

(iv)

The remainder is 61.
It represents that square of 42 is less than in 1825.
Next number is 43 and 43² = 1849
Hence, number to be added to 1825 = 1849 – 1825 = 24
The required perfect square is 1848 and √1849 =43

(v)

Here, the remainder is 12.
It represents that a square of 80 is less than in 6412.
The next number is 81 and 81² = 6561
Hence the number to be added = 6561 – 6412 = 149
The require perfect square is 6561 and √6561 = 81

Ex 6.4 Class 8 Maths Question 6.
Find the length of the side of a square whose area = 441 m²
Solution:
Let the length of the side of the square be x m.
Area of the square = (side)² = x² m²
x² = 441 ⇒ x = √441 = 21

Thus, x = 21 m.
Hence the length of the side of square = 21 m.

Ex 6.4 Class 8 Maths Question 7.
In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC = 13 cm, BC = 5 cm, find AB
Solution:
(a) In right triangle ABC

AC² = AB² + BC² [By Pythagoras Theorem]
⇒ AC² = (6)² + (8)² = 36 + 64 = 100
⇒ AC = √100 = 10
Thus, AC = 10 cm.
(b) In right triangle ABC

AC² = AB² + BC² [By Pythagoras Theorem]
⇒ (13)² = AB² + (5)²
⇒ 169 = AB² + 25
⇒ 169 – 25 = AB²
⇒ 144 = AB²
AB = √144 = 12 cm
Thus, AB = 12 cm.

Ex 6.4 Class 8 Maths Question 8.
A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain the same. Find the minimum number of plants he needs more for this.
Solution:
Let the number of rows be x.
And the number of columns also be x.
Total number of plants = x × x = x²
x² = 1000 ⇒ x = √1000

Here the remainder is 39
So the square of 31 is less than 1000.
Next number is 32 and 32² = 1024
Hence the number to be added = 1024 – 1000 = 24
Thus the minimum number of plants required by him = 24.
Alternative method:

The minimum number of plants required by him = 24.

Ex 6.4 Class 8 Maths Question 9.
There are 500 children in a school. For a P.T. drill, they have to stand in such a manner that the number of rows is equal to the number of columns. How many children would be left out in this arrangement?
Solution:
Let the number of children in a row be x. And also that of in a column be x.
Total number of students = x × x = x²
x² = 500 ⇒ x = √500

Here the remainder is 16
New Number 500 – 16 = 484
and, √484 = 22
Thus, 16 students will be left out in this arrangement.

Extra Questions

Squares and Square Roots Class 8 Extra Questions Maths Chapter 6

Extra Questions for Class 8 Maths Chapter 6 Squares and Square Roots

Squares and Square Roots Class 8 Extra Questions

Question 1.
Find the perfect square numbers between 40 and 50.
Solution:
Perfect square numbers between 40 and 50 = 49.

Question 2.
Which of the following 24², 49², 77², 131² or 189² end with digit 1?
Solution:
Only 49², 131² and 189² end with digit 1.

Question 3.
Find the value of each of the following without calculating squares.
(i) 27² – 26²
(ii) 118² – 117²
Solution:
(i) 27² – 26² = 27 + 26 = 53
(ii) 118² – 117² = 118 + 117 = 235

Question 4.
Write each of the following numbers as difference of the square of two consecutive natural numbers.
(i) 49
(ii) 75
(iii) 125
Solution:
(i) 49 = 2 × 24 + 1
49 = 25² – 24²
(ii) 75 = 2 × 37 + 1
75 = 38² – 37²
(iii) 125 = 2 × 62 + 1
125 = 63² – 62²

Question 5.
Write down the following as sum of odd numbers.
(i) 7²
(ii) 9²
Solution:
(i) 7² = Sum of first 7 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii) 9² = Sum of first 9 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17

Question 6.
Express the following as the sum of two consecutive integers.
(i) 15²
(ii) 19²
Solution:

Question 7.
Find the product of the following:
(i) 23 × 25
(ii) 41 × 43
Solution:
(i) 23 × 25 = (24 – 1) (24 + 1) = 24² – 1 = 576 – 1 = 575
(ii) 41 × 43 = (42 – 1) (42 + 1) = 42² – 1 = 1764 – 1 = 1763

Question 8.
Find the squares of:
(i) 
(ii) 
Solution:

Question 9.
Check whether (6, 8, 10) is a Pythagorean triplet.
Solution:
2m, m² – 1 and m² + 1 represent the Pythagorean triplet.
Let 2m = 6 ⇒ m = 3
m² – 1 = (3)² – 1 = 9 – 1 = 8
and m² + 1 = (3)² + 1 = 9 + 1 = 10
Hence (6, 8, 10) is a Pythagorean triplet.
Alternative Method:
(6)² + (8)² = 36 + 64 = 100 = (10)²
⇒ (6, 8, 10) is a Pythagorean triplet.

Question 10.
Using property, find the value of the following:
(i) 19² – 18²
(ii) 23² – 22²
Solution:
(i) 19² – 18² = 19 + 18 = 37
(ii) 23² – 22² = 23 + 22 = 45

Squares and Square Roots Class 8 Extra Questions Short Answer Type

Question 11.
Using the prime factorisation method, find which of the following numbers are not perfect squares.
(i) 768
(ii) 1296
Solution:

768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, 3 is not in pair.
768 is not a perfect square.

1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
Here, there is no number left to make a pair.
1296 is a perfect square.

Question 12.
Which of the following triplets are Pythagorean?
(i) (14, 48, 50)
(ii) (18, 79, 82)
Solution:
We know that 2m, m² – 1 and m² + 1 make Pythagorean triplets.
(i) For (14, 48, 50),
Put 2m =14 ⇒ m = 7
m² – 1 = (7)² – 1 = 49 – 1 = 48
m² + 1 = (7)² + 1 = 49 + 1 = 50
Hence (14, 48, 50) is a Pythagorean triplet.
(ii) For (18, 79, 82)
Put 2m = 18 ⇒ m = 9
m² – 1 = (9)² – 1 = 81 – 1 = 80
m² + 1 = (9)² + 1 = 81 + 1 = 82
Hence (18, 79, 82) is not a Pythagorean triplet.

Question 13.
Find the square root of the following using successive subtraction of odd numbers starting from 1.
(i) 169
(ii) 81
(iii) 225
Solution:
(i) 169 – 1 = 168, 168 – 3 = 165, 165 – 5 = 160, 160 – 7 = 153, 153 – 9 = 144, 144 – 11 = 133, 133 – 13 = 120, 120 – 15 = 105, 105 – 17 = 88, 88 – 19 = 69,
69 – 21 = 48, 48 – 23 = 25, 25 – 25 = 0
We have subtracted odd numbers 13 times to get 0.
√169 = 13
(ii) 81 – 1 = 80, 80 – 3 = 77, 77 – 5 = 72, 72 – 7 = 65, 65 – 9 = 56, 56 – 11 = 45, 45 – 13 = 32, 32 – 15 = 17, 17 – 17 = 0
We have subtracted 9 times to get 0.
√81 = 9
(iii) 225 – 1 = 224, 224 – 3 = 221, 221 – 5 = 216, 216 – 7 = 209, 209 – 9 = 200, 200 – 11 = 189, 189 – 13 = 176, 176 – 15 = 161, 161 – 17 = 144, 144 – 19 = 125,
125 – 21 = 104, 104 – 23 = 81, 81 – 25 = 56, 56 – 27 = 29, 29 – 29 = 0
We have subtracted 15 times to get 0.
√225 = 15

Question 14.
Find the square rootofthe following using prime factorisation
(i) 441
(ii) 2025
(iii) 7056
(iv) 4096
Solution:
(i) 441 = 3 × 3 × 7 × 7
√441 = 3 × 7 = 21

(ii) 2025 = 3 × 3 × 3 × 3 × 5 × 5
√2025 = 3 × 3 × 5 = 45

(iii) 7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
√7056 = 2 × 2 × 3 × 7 = 84

(iv) 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
√4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64

Question 15.
Find the least square number which is divisible by each of the number 4, 8 and 12.
Solution:
LCM of 4, 8, 12 is the least number divisible by each of them.
LCM of 4, 8 and 12 = 24
24 = 2 × 2 × 2 × 3
To make it perfect square multiply 24 by the product of unpaired numbers, i.e., 2 × 3 = 6
Required number = 24 × 6 = 144

Question 16.
Find the square roots of the following decimal numbers
(i) 1056.25
(ii) 10020.01
Solution:

Question 17.
What is the least number that must be subtracted from 3793 so as to get a perfect square? Also, find the square root of the number so obtained.
Solution:
First, we find the square root of 3793 by division method.

Here, we get a remainder 72
61² < 3793
Required perfect square number = 3793 – 72 = 3721 and √3721 = 61

Question 18.
Fill in the blanks:
(а) The perfect square number between 60 and 70 is …………
(b) The square root of 361 ends with digit …………..
(c) The sum of first n odd numbers is …………
(d) The number of digits in the square root of 4096 is ………..
(e) If (-3)² = 9, then the square root of 9 is ……….
(f) Number of digits in the square root of 1002001 is …………
(g) Square root of  is ………..
(h) The value of √(63 × 28) = …………
Solution:
(a) 64
(b) 9
(c) n²
(d) 2
(e) ±3
(f) 4
(g) 
(h) 42

Question 19.
Simplify: √900 + √0.09 + √0.000009
Solution:
We know that √(ab) = √a × √b
√900 = √(9 × 100) = √9 × √100 = 3 × 10 = 30
√0.09 = √(0.3 × 0.3) = 0.3
√0.000009 = √(0.003 × 0.003) = 0.003
√900 + √0.09 + √0.000009 = 30 + 0.3 + 0.003 = 30.303

Squares and Square Roots Class 8 Extra Questions Higher Order Thinking Skills (HOTS)

Question 20.
Find the value of x if

Solution:

Question 21.
Simplify:

Solution:

Question 22.
A ladder 10 m long rests against a vertical wall. If the foot of the ladder is 6 m away from the wall and the ladder just reaches the top of the wall, how high is the wall? (NCERT Exemplar)

Solution:
Let AC be the ladder.
Therefore, AC = 10 m
Let BC be the distance between the foot of the ladder and the wall.
Therefore, BC = 6 m
∆ABC forms a right-angled triangle, right angled at B.
By Pythagoras theorem,
AC² = AB² + BC²
10² = AB² + 6²
or AB² = 10² – 6² = 100 – 36 = 64
or AB = √64 = 8m
Hence, the wall is 8 m high.

Question 23.
Find the length of a diagonal of a rectangle with dimensions 20 m by 15 m. (NCERT Exemplar)
Solution:
Using Pythagoras theorem, we have Length of diagonal of the rectangle =  units

Hence, the length of the diagonal is 25 m.

Question 24.
The area of a rectangular field whose length is twice its breadth is 2450 m2. Find the perimeter of the field.
Solution:
Let the breadth of the field be x metres. The length of the field 2x metres.
Therefore, area of the rectangular field = length × breadth = (2x)(x) = (2x²) m²
Given that area is 2450 m².
Therefore, 2x² = 2450
⇒ x² = 1225
⇒ x = √1225 or x = 35 m
Hence, breadth = 35 m
and length = 35 × 2 = 70 m
Perimeter of the field = 2 (l + b ) = 2(70 + 35) m = 2 × 105 m = 210 m.

NCERT Solutions for Class 8 Maths

• Chapter 1: Rational Numbers
• Chapter 2: Linear Equations in One Variable
• Chapter 3: Understanding Quadrilaterals
• Chapter 4: Practical Geometry
• Chapter 5: Data Handling
• Chapter 6: Squares and Square Roots
• Chapter 7: Cubes and Cube Roots
• Chapter 8: Comparing Quantities
• Chapter 9: Algebraic Expressions and Identities
• Chapter 10: Visualising Solid Shapes
• Chapter 11: Mensuration
• Chapter 12: Exponents and Powers
• Chapter 13: Direct and Indirect proportions
• Chapter 14: Factorisation
• Chapter 15: Introduction to Graphs
• Chapter 16: Playing with Numbers